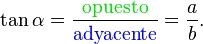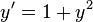jueves, 26 de mayo de 2011

FUNCIONES TRIGONOMETRICAS

Función trigonométrica

De Wikipedia, la enciclopedia libre

Las funciones trigonométricas, en matemáticas, son relaciones angulares que se utilizan para relacionar los ángulos del triángulo con las longitudes de los lados del mismo según los principios de la Trigonometría.
Las funciones trigonométricas son de gran importancia en física, astronomía, cartografía, náutica, telecomunicaciones, la representación de fenómenos periódicos, y otras muchas aplicaciones.

Todas las funciones trigonométricas de un ángulo θ pueden ser construidas geométricamente en relación a una circunferencia de radio unidad de centro O.

Contenido

[ocultar]

[editar] Conceptos básicos

Identidades trigonométricas fundamentales.

Las Razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos.
Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones, aunque se pueden definir geométricamente o por medio de sus relaciones. Algunas funciones fueron comunes antiguamente, y aparecen en las primeras tablas, pero no se utilizan actualmente; por ejemplo el verseno (1 − cos θ) y la exsecante (sec θ − 1).

Función	Abreviatura	Equivalencias (en radianes)
Seno	sin (sen)	$\sin \; \theta \equiv \frac{1}{\csc \theta} \equiv \cos \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\cos \theta}{\cot \theta} \,$
Coseno	cos	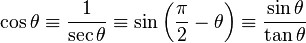$\cos \theta \equiv \frac{1}{\sec \theta} \equiv \sin \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\sin \theta}{\tan \theta} \,$
Tangente	tan	$\tan \theta \equiv \frac{1}{\cot \theta} \equiv \cot \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\sin \theta}{\cos \theta} \,$
Cotangente	ctg	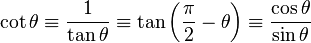$\cot \theta \equiv \frac{1}{\tan \theta} \equiv \tan \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\cos \theta}{\sin \theta} \,$
Secante	sec	$\sec \theta \equiv \frac{1}{\cos \theta} \equiv \csc \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\tan \theta}{\sin \theta} \,$
Cosecante	csc (cosec)	$\csc \theta \equiv \frac{1}{\sin \theta} \equiv \sec \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\cot \theta}{\cos \theta} \,$

[editar] Definiciones respecto de un triángulo rectángulo

Para definir las razones trigonométricas del ángulo:

α

, del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:

La hipotenusa es el lado opuesto al ángulo recto, o lado de mayor longitud del triángulo rectángulo.
El [[Cateto|cateto opuesto] es el lado opuesto al ángulo que queremos determinar.
El [[Cateto|cateto adyacente]es el lado adyacente al ángulo del que queremos determinar.

Todos los triángulos considerados se encuentran en el Plano Euclidiano, por lo que la suma de sus ángulos internos es igual a π radianes (o 180°). En consecuencia, en cualquier triángulo rectángulo los ángulos no rectos se encuentran entre 0 y π/2 radianes. Las definiciones que se dan a continuación definen estrictamente las funciones trigonométricas para ángulos dentro de ese rango:
1) El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa:

$\sin \alpha = \frac {{ \color{ForestGreen}\textrm{opuesto}}} {{ \color{Red}\textrm{hipotenusa}}} = \frac {a} {h}.$

El valor de esta relación no depende del tamaño del triángulo rectángulo que elijamos, siempre que tenga el mismo ángulo

α

, en cuyo caso se trata de triángulos semejantes.
2) El coseno de un ángulo es la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa:

$\cos \alpha = \frac {{ \color{Blue}\textrm{adyacente}}} {{ \color{Red}\textrm{hipotenusa}}} = \frac {b} {h}.$

3) La tangente de un ángulo es la relación entre la longitud del cateto opuesto y la del adyacente:

$\tan \alpha = \frac {{ \color{ForestGreen}\textrm{opuesto}}} {{ \color{Blue}\textrm{adyacente}}} = \frac {a} {b}.$

4) La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto:

$\cot \alpha = \frac {{ \color{Blue}\textrm{adyacente}}} {{ \color{ForestGreen}\textrm{opuesto}}} = \frac {b} {a}.$

5) La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente:

$\sec \alpha = \frac {{ \color{Red}\textrm{hipotenusa}}} {{ \color{Blue}\textrm{adyacente}}} = \frac {h} {b}.$

6) La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto:

$\csc \alpha = \frac {{ \color{Red}\textrm{hipotenusa}}} {{ \color{ForestGreen}\textrm{opuesto}}} = \frac {h} {a}.$

[editar] Funciones trigonométricas de ángulos notables

Animación de la función seno.

	0°	30°	45°	60°	90°
sen	0	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	1
cos	1	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	0
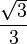tan	0	$\frac{\sqrt{3}}{3}$	1	$\sqrt{3}$	$\infty$

[editar] Representación gráfica

[editar] Definiciones analíticas

La definición analítica más frecuente dentro del análisis real se hace a partir de ecuaciones diferenciales. Usando la geometría y las propiedades de los límites, se puede demostrar que la derivada del seno es el coseno y la derivada del coseno es el seno con signo negativo. (Aquí, como se hace generalmente en cálculo, todos los ángulos son medidos en radianes.)

$\begin{cases} S'(x) = C(x) & S(0) = 0 \\ C'(x) = -S(x)& C(0) = 1 \end{cases}$

El teorema de Picard-Lindelöf de existencia y unicidad de las ecuaciones diferenciales lleva a que existen las funciones anteriores que se llaman respectivamente seno y coseno, es decir:

$\cos x = C(x), \qquad \sin x = S(x)$

Esta definición analítica de las funciones trigonométricas permite una definición no-geométrica del número π, a saber, dicho número es el mínimo número real positivo que es un cero de la función seno.

[editar] Series de potencias

A partir de las definición anterior pueden establecerse que las funciones seno y coseno son funciones analíticas cuya serie de Maclaurin viene dada por:

$\sin x = \sum_{k=0}^\infty \cfrac{(-1)^k \; x^{2k+1}}{(2k+1)!} = \cfrac{x}{1!} - \cfrac{x^3}{3!} + \cfrac{x^5}{5!} - \cfrac{x^7}{7!} \; \dots$

$\cos x = \sum_{k=0}^\infty \cfrac{(-1)^k \; x^{2k}}{(2k)!} = \cfrac{1}{0!} - \cfrac{x^2}{2!} + \cfrac{x^4}{4!} - \cfrac{x^6}{6!} \; \dots$

Estas identidades son aveces usadas como las definiciones de las funciones seno y coseno. Con frecuencia se utilizan como el punto de partida para el tratamiento riguroso de las funciones trigonométricas y sus aplicaciones (por ejemplo en las Series de Fourier), debido a que la teoría de las series infinitas puede ser desarrollada a partir de la base del sistema de números reales, independientemente de cualquier consideración geométrica. La diferenciabilidad y continuidad de estas funciones es entonces establecida a partir de las definiciones de series por si misma.

[editar] Relación con la exponencial compleja

Existe una relación importante entre la exponenciación de números complejos y las funciones trigonométricas:

$e^{ix} = \cos x + i \sin x \,$

Esta relación puede probarse usando el desarrollo en serie de Taylor para la función exponencial y el obtenido en la sección anterior para las funciones seno y coseno. Separando ahora en parte real e imaginaria en la expresión anterior se encuentran las definiciones de seno y coseno en términos de exponenciales complejas:

$\cos x = \frac{e^{ix}+e^{-ix}}{2} \qquad \sin x = \frac{e^{ix}-e^{-ix}}{2i}$

[editar] A partir de ecuaciones diferenciales

Las funciones seno y coseno satisfacen la igualdad:

$y'' = -y.\,$

Es decir, la segunda derivada de cada función es la propia función con signo inverso. Dentro del espacio funcional de dos dimensiones V, que consiste en todas las soluciones de esta ecuación,

la función seno es la única solución que satisface la condición inicial $\scriptstyle \left( y'(0), y(0) \right) = (1, 0)\,$ y
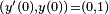la función coseno es la única solución que satisface la condición inicial $\scriptstyle \left( y'(0), y(0) \right) = (0, 1)\,$ .

Dado que las funciones seno y coseno son linearmente independientes, juntas pueden formar la base de V. Este método para definir las funciones seno y coseno es esencialmente equivalente a utilizar la fórmula de Euler. Además esta ecuación diferencial puede utilizarse no solo para definir al seno y al coseno, con ella también se pueden probar las identidades trigonométricas de las funciones seno y coseno.
Además, la observación de que el seno y el coseno satisfacen y′′ = −y implica que son funciones eigen del operador de la segunda derivada.
La función tangente es la única solución de la ecuación diferencial no lineal

$y' = 1 + y^2\,$

satisfaciendo la condición inicial y(0) = 0. Existe una interesante prueba visual de que la función tangente satisface esta ecuación diferencial.

[editar] Funciones trigonométricas inversas

Las tres funciones trigonométricas inversas comúnmente usadas son:

Arcoseno es la función inversa del seno de un ángulo. El significado geométrico es: el arco cuyo seno es dicho valor.

La función arcoseno real es una función $\left[-1,1\right] \to \left[0,2\pi \right)\,$ , es decir, no está definida para cualquier número real. Esta función puede expresarse mediante la siguiente serie de Taylor:

$\mbox{arcsin}(x) = \begin{cases} -\cfrac{\pi}{2} & x = -1 \\ x + \cfrac{1}{2}\cfrac{x^3}{3} + \cfrac{1\cdot 3}{2\cdot 4}\cfrac{x^5}{5} + \cfrac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\cfrac{x^7}{7} + \dots & -1 < x < 1\\ +\cfrac{\pi}{2} & x = 1 \end{cases}$

Arcocoseno es la función inversa del coseno de un ángulo. El significado geométrico es: el arco cuyo coseno es dicho valor.

Es una función similar a la anterior, de hecho puede definirse como:

$\mbox{arccos}(x) = \frac{\pi}{2} - \mbox{arcsin}(x)$

Arcotangente es la función inversa de la tangente de un ángulo. El significado geométrico es: el arco cuya tangente es dicho valor.

A diferencia de las anteriores la función arcotangente está definida para todos los reales. Su expresión en forma de serie es:

$\mbox{arctan}(x) = \begin{cases} x - \cfrac{x^3}{3} + \cfrac{x^5}{5} - \cfrac{x^7}{7} + \dots & |x| < 1 \\ \pm\cfrac{\pi}{2} -\cfrac{1}{x} +\cfrac{1}{3x^3} -\cfrac{1}{5x^5}+ \dots & +\ \mbox{con}\ x \ge 1, -\ \mbox{con}\ x \le -1 \end{cases}$

[editar] Generalizaciones

Las funciones hiperbólicas son el análogo de las funciones trigonométricas para una hipérbola equilatera. Además el seno y coseno de un número imaginario puro puede expresarse en términos de funciones hiperbólicas.
Las funciones elípticas son una generalización biperiódica de las funciones trigonométricas que en el plano complejo sólo son periódicas sobre el eje real. En particular las funciones trigonométricas son el límite de las funciones elípticas de Jacobi cuando el parámetro del que dependen tiende a cero.

[editar] Historia

Artículo principal: Historia de la trigonometría

El estudio de las funciones trigonométricas se remonta a la época de Babilonia, y gran parte de los fundamentos de trigonometría fueron desarrollados por los matemáticos de la Antigua Grecia, de la India y estudiosos musulmanes.
El primer uso de la función seno (sin(·)) aparece en el Sulba Sutras escrito en India del siglo VIII al VI a. C. Las funciones trigonométricas fueron estudiadas por Hiparco de Nicea (180-125 a. C.), Aryabhata (476-550), Varahamihira, Brahmagupta, al-Khwarizmi, Abu'l-Wafa, Omar Khayyam, Bhaskara II, Nasir al-Din Tusi, Regiomontanus (1464), Ghiyath al-Kashi y Ulugh Beg (Siglo XIV), Madhava (ca. 1400), Rheticus, y el alumno de éste, Valentin Otho. La obra de Leonhard Euler Introductio in analysin infinitorum (1748) fue la que estableció el tratamiento analítico de las funciones trigonométricas en Europa, definiéndolas como series infinitas presentadas en las llamadas "Fórmulas de Euler".
La noción de que debería existir alguna correspondencia estándar entre la longitud de los lados de un triángulo siguió a la idea de que triángulos similares mantienen la misma proporción entre sus lados. Esto es, que para cualquier triángulo semejante, la relación entre la hipotenusa y otro de sus lados es constante. Si la hipotenusa es el doble de larga, así serán los catetos. Justamente estas proporciones son las que expresan las funciones trigonométricas

NUMEROS ENTEROS

Número entero

De Wikipedia, la enciclopedia libre

Saltar a navegación, búsqueda

Resta con negativos. La resta de dos números naturales no es un número natural cuando el sustraendo es mayor que el minuendo, sino que su valor es negativo: en la imagen, sólo pueden sustraerse 3 plátanos, por lo que se apunta un plátano "debido" o "negativo" (en rojo).

Los números enteros son un conjunto de números que incluye a los números naturales distintos de cero (1, 2, 3, ...), los negativos de los números naturales (..., −3, −2, −1) y al cero, 0. Los enteros negativos, como −1 ó −3 (se leen "menos uno", "menos tres", etc.), son menores que todos los enteros positivos (1, 2, ...) y que el cero. Para resaltar la diferencia entre positivos y negativos, a veces también se escribe un signo "más" delante de los positivos: +1, +5, etc.
El conjunto de todos los números enteros se representa por la letra ℤ = {..., −3, −2, −1, 0, +1, +2, +3, ...}, que proviene del alemán Zahlen ("números", pronunciado [ˈtsaːlən]).
Los números enteros no tienen parte decimal. Por ejemplo:

−783 y 154 son números enteros

45,23 y −34/95 no son números enteros

Al igual que los números naturales, los números enteros pueden sumarse, restarse, multiplicarse y dividirse, de forma similar a los primeros. Sin embargo, en el caso de los enteros es necesario calcular también el signo del resultado.
Los números enteros extienden la utilidad de los números naturales para contar cosas. Pueden utilizarse para contabilizar pérdidas: si en un colegio entran 80 alumnos nuevos de primer curso un cierto año, pero hay 100 alumnos de último curso que pasaron a educación secundaria, en total habrá 100 − 80 = 20 alumnos menos; pero también puede decirse que dicho número ha aumentado en 80 − 100 = −20 alumnos.
También hay ciertas magnitudes, como la temperatura o la altura toman valores por debajo del cero. La altura del Everest es 8848 metros por encima del nivel del mar, y por el contrario, la orilla del Mar Muerto está 423 metros por debajo del nivel del mar; es decir, su altura se puede expresar como −423 m

CONJUNTO Y SU CLASIFICACION

¿Qué es un conjunto?

Es la agrupación en un todo de objetos bien diferenciados en el la mente o en la intuición, por lo tanto, estos objetos son bien determinados y diferenciados.
Es la reunión, agrupación o colección de elementos bien definidos que tienen una propiedad en común, este fue inventado por Georg Cantor hace 100 años. Sus conceptos han penetrado y transformado todas las teorías formales y todas las ramas de la matemática y de la lógica, así como la misma ontología.

Como este es un concepto primario, el conjunto no puede definirse; sólo se puede dar una idea intuitiva de el.

A pesar de su sencillez este concepto es la base de las Matemáticas actuales, ya que, entre otras cosas, sirve para la construcción de los números. Sirve además para estudiar las estructuras algebraicas, con las cuales se organizan ordenadamente todos los conocimientos matemáticos.
Ejemplos: los alumnos de un colegio, los números impares, los meses del año, etc., siendo cada alumno del colegio, cada número impar, cada mes del año, respectivamente, elementos de cada uno de los correspondientes conjuntos.
¿Qué es un elemento?

Elemento es cada uno de los objetos por los cuales esta conformado un conjunto.
Por ejemplo, par los ejemplos tomados anteriormente en el concepto de conjunto. Luis, Antonio, Paula, son los elementos del primer conjunto, por que ellos son alumnos de colegio. 1,3,5 son elementos del segundo conjunto porque son números impares.

Este ejemplo gráfico nos muestra la agrupación llamado Alumnos de Colegio con sus elementos que serían: Luis, Antonio, Paula y Pánfilo
¿Cuáles son las formas de determinar un conjunto?

Un conjunto puede determinarse de dos formas:

Por extensión: escribiendo dentro de una llave los nombres de los elementos del conjunto.

Por comprensión: escribiendo dentro de una llave una propiedad característica de los elementos del conjunto y solamente de ellos.

Ejemplo: El conjunto de los meses del año se nombra:
Por extensión: {Enero, febrero, marzo, abril, mayo, junio, julio, agosto, septiembre, octubre, noviembre, diciembre}
Por comprensión: {meses del año}, o bien, de esta otra forma: {x/x es un mes del año}, que se lee: conjunto de elementos x tales que x es un mes del año.
Ejemplo: El conjunto dedos de la mano se nombra
Por extensión: {Pulgar, Indice, Mayor, Anular, meñique}
Por comprensión: {dedos de la mano}, o bien, de esta otra forma: {x/x es dedo de la mano}, que se lee: conjunto de elementos x tales que x es un dedo de la mano
¿Qué es la relación de pertenencia?
Es la relación que existe entre un elemento y un conjunto, así, un elemento pertenece al conjunto, y se representa de esta forma.

Ejemplo, A = {x/x es dedo de la mano}
B= índice, entonces

Cuando un elemento no esta en el conjunto dicho elemento no pertenece al conjunto, y se representa de la siguiente manera

Ejemplo, A = {x/x es mes del año}
B= índice, entonces

Señale los tipos de conjuntos que conoce
Conjunto Finito: Se denomina así al conjunto al cual podemos nombrar su último elemento
Ejemplo: M={x/x es mes del año}
Por que sabemos que el último mes es Diciembre
Conjunto Infinito: Se denomina así al conjunto al cual no podemos nombrar su último elemento
Ejemplo: M={x/x es número natural}
Por que no sabemos que cual es el último mes es el último número
Conjunto Universo: Se denomina así al conjunto formado por todos los elementos del tema de referencia
Ejemplo: U={x/x es un animal}
A={x/x es un mamífero}
B={x/x es un reptil}
Conjunto vacío: Se denomina así al conjunto que no tiene ningún elemento. A pesar de no tener elementos se le considera como conjunto y se representa de la siguiente forma: {*}
Ejemplos: Conjunto de los meses del año que terminan en a.
Conjunto de números impares múltiplos de 2.

Conjunto unitario. Es el conjunto que tiene un solo elemento.

Ejemplo: Conjunto de los meses del año que tiene menos de reinta días, solamente febrero pertenece a dicho conjunto.
Conjuntos disjuntos. Se llaman conjuntos disjuntos aquellos que no tienen ningún elemento que pertenezca a ambos al mismo tiempo.
Ejemplo: Los dos conjuntos siguientes:
{x/x es un número natural}
{x/x es un día de la semana}
son disjuntos ya que no tienen ningún elemento común.
Conjunto de las partes de un conjunto: Se llama así al conjunto formado por todos los subconjuntos posibles de un conjunto dado. Observamos que en él los elementos son, a su vez, conjuntos. Se representan por p(A).
Ejemplo: Dado el conjunto: A={a,b,c,d.}
Formemos todos sus subconjuntos: , M={a}, N={b}, P={c}, Q={d}, R={a,c}, T={a,d}, U={b,c}, V={b,d}, X={c,d}, Y={a,b,c}, Z={a,b,d}, L={b,c,d}. El conjunto de las partes de A, es decir (A), será:
p(A) = {{ }, M, N, P, Q, R, S, T, U, V, X, Y, Z, L, A}
¿Qué es un conjunto universo?
Conjunto Universo: Se denomina así al conjunto formado por todos los elementos del tema de referencia
Ejemplo: U={x/x es un animal}
A={x/x es un mamífero}
B={x/x es un reptil}
¿Cuándo dos conjuntos son iguales?
Dos conjuntos son iguales si, y solamente si, todos los elementos del primero son iguales a los elementos del segundo y todo elemento del segundo es elemento del primero.
Ejemplo: Los dos siguientes conjuntos: {x/x es un número natural} {x/x es un número entero positivo} son iguales, ya que todo número entero positivo es un número natural.
¿Cuándo establece la inclusión o contenencia entre dos conjuntos?
El conjunto A esta incluido en B si todos los elementos del conjunto A pertenecen al conjunto B, y se escribe:

A esta incluido en B
1. Propiedad reflexiva: Todo conjunto está incluido en si mismo. Esto se expresa de la siguiente forma: VA =>, A cA que se lee: «para todo conjunto A se verifica que A está incluido en A».
2. Propiedad antisimétrica: Dados dos conjuntos diferentes A y B, si A está incluido en B, B no puede estar incluido en A. Es decir: Si y A diferente B y A c B =gt B NO c A
3. Propiedad transitiva: Si un conjunto A está incluido en otro conjunto B y a su vez B esta incluido en C, A esta incluido en C. Sean los conjuntos:
A={a,b,c}; B={a,b,c,d,n}; C={a,b,c,d,n,m}.
en los cuales se observa con claridad que si los elementos del conjunto A son elementos del conjunto B, y los del conjunto B son también elementos del conjunto C, los elementos de A serán elementos de C.
¿Qué son los diagramas de Venn?
Es la representación gráfica de un conjunto en la cual se sitúan dentro de una línea cerrada los signos representativos de los elementos del conjunto. En la figura se muestran las dos formas respectivas de representar el conjunto: A= {a, b, c, d, e}.
¿Cuáles son las operaciones entre conjuntos?

Unión de conjuntos. Es la unión de los elementos de dos o mas conjuntos, formando un nuevo conjunto cuyos elementos son los elementos de los conjuntos originales, pero, cuando un elemento se repite, dicho elemento entrará a formar parte del conjunto unión una sola vez; en esto se diferencia la unión de conjuntos del concepto clásico de la suma, en la que los elementos comunes se consideran tantas veces como estén en el total de los conjuntos.
Ejemplo: Dados los conjuntos: A = {d, f g, h} y B = {b, c, d, f}
La unión de dichos conjuntos será: AUB= {d, f, g, h, b, c}
, mientras que según el concepto clásico de la suma hubiésemos puesto:
A + B = d + f + g + h + b + c + d + f.

Propiedades de la unión de conjuntos:
1. Propiedad idempotente. Puede exponerse mediante la siguiente expresión, que por ser tan lógica, no necesita más explicación:

VA => A = A

2. Propiedad conmutativa. Es también evidente:

AUB = BUA

3. Propiedad asociativa. Dados tres conjuntos A, B y C se verifica que:

(AUB)UC = AU(BUC) = AUBUC

Se puede demostrar mediante un ejemplo sencillo. Sean: A = {m, n, p}, B ={j, k, l}, C = {r, p, l}.
El nuevo conjunto y éste unido con el conjunto C, dará como resultado el conjunto: (AUB)UC = {m, n, p,j,k,l,r}
ahora bien, si hacemos antes la unión de B con C tendremos: BUC = {j,k,l,r,p} que unido con el conjunto A nos da: AU(BUC) = {m, n, p, j,k,l,r,p}
Luego, los conjuntos (AUB)UC y AU(BUC) son iguales por estar formados por los mismos elementos.
Intersección de conjuntos. Se llama intersección de dos conjuntos A y B, y se representa por AnB, al nuevo conjunto que tiene por elementos todos los elementos comunes a A y a B. Es lógico que la intersección de dos conjuntos disjuntos sea el conjunto vacío (no tiene elementos).
Ejemplo: Dados los conjuntos A = { d, f g, h } y B = { b, c, d, f }, su intersección será: AnB = {d,f}
La representación gráfica de dicha intersección esta representada en la figura, en la cual la intersección es la parte rayada.
Propiedades de la intersección. Son las mismas que las de la unión; por tanto, las expresaremos de la forma siguiente:
1. Propiedad idempotente: VA => AnA = A
2. Propiedad conmutativa: AnB = BnA

Propiedad asociativa: (AnB)nC = An(BnC)

Propiedades comunes a la unión y a la intersección.

Ley de absorción. Tiene dos formas distintas que se expresan: An(AUB) = A y Au(BnC)

Expongamos un ejemplo como comprobación:
A = {1, 2, 3 , 4} y B = {1, 2, 3, 6}.
Hagamos primero la unión de A con B: AUB = {1,2,3,4,6}
y ahora, la intersección del mismo con el conjunto
A: An(AUB) = {1, 2, 3 , 4} = A
Análogamente:
AnB = {1, 2, 3}, AU(AnB) = {1, 2, 3 , 4} = A B) = { 1,2, 3, 4 } = A.
2. Ley distributiva. Tiene también dos formas de expresión: De la unión respecto de la intersección: (AnC)UC = (AUC)n(BUC)
De la intersección respecto de la unión: (AUB)nC = (AnC)U(BnC)
Estas dos propiedades comunes a las dos operaciones nos indican que ambas tienen la misma fuerza, existe entre ellas una completa analogía.
Diferencia de conjuntos y complementario de un conjunto con respecto a otro. Dados dos conjuntos A y B, se llama diferencia de A para B, y se representa por A - B al conjunto de todos los elementos de A que no son elementos de B. Ejemplo: Si A = {a, b, j c, d, e} y B={a, b, m, n, p}, A - B ={c, d, e.}. Dicho ejemplo está representado en la figura (A) en la que se comprueba que esta diferencia no goza de la propiedad conmutativa.

Si A es un subconjunto de B, se llama complementario de A y se representa por:
[A, al conjunto formado por todos los elementos que pertenecen a B y no pertenecen a A.]
Como vemos, se trata de dos conceptos similares, pero que no hay que confundir.

Producto cartesiano de dos conjuntos. Se llama conjunto producto cartesiano de dos conjuntos A y B, y se representa por A x B, al conjunto formado por todos los pares ordenados de elementos (a, b), tales que a A y b B.

Al decir «pares ordenados», estamos definiendo un nuevo concepto nuevo hasta ahora, y que al ser ordenados, serán diferentes los pares: (a, b) y (b, a), lo cual nos indica a su vez que dicho producto cartesiano no goza de la propiedad conmutativa. En efecto, al considerar, por ejemplo, los conjuntos: A = {a, b, c, d, e} y B = {m, n} podemos hallar el producto cartesiano de A x B, resultando: A x B = {(a, m), (a, n), (b, m), (b, n), (c, m), (c, n), (e, m), (e, n).}.
Sin embargo, si hallamos el producto cartesiano de B x A:
B x A = {(m, a), (m, b), (m, c), (m, d), (m, e), (n, a), (n, b), (n, c), (n, d), (n, e).}. observándose que en ellos los pares son diferentes, pues aunque están formados por los mismos elementos, están en distinto orden.
Propiedades del producto cartesiano.
1. El producto cartesiano de un conjunto. Cualquiera por el conjunto vacío da como resultado el conjunto vacío. Ax{ } = { }
es evidente, ya que el conjunto vacío carece de elementos, luego no se pueden formar pares con los del otro conjunto A.
2. Propiedad distributiva respecto de la unión. Se expresa: A(BUC) = (AxB)U(AxC)

Propiedad distributiva respecto de la intersección: Ax(BnC) = ((AxB)n(AxC))